Answer:
there is 15
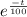 amount of salt in the tank after t minute.
amount of salt in the tank after t minute.
Explanation:
Given the data in the question;
tank contains 1000L of brine with 20kg of dissolved salt, Pure water enters the tank at a rate of 15L/min.
How much salt is in the tank after t minutes.
Now,
let x represent the amount of salt after t minutes,
so
x(0) = 15
dx/dt = rate in - rate out
Now, since the water entering is pure, the rate in is 0
rate out will be; x/1000 × 10 kg
∴
dx/dt = -x/100
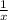 dx = -
dx = -
 dt
dt
∫
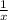 dx = -
dx = -
 ∫1dt + c
∫1dt + c
lnx = -
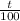 + c
+ c
Now since x(0) = 15
ln15 = c
lnx = -
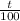 + ln15
+ ln15
x =
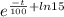
x = 15
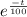
Therefore, there is 15
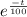 amount of salt in the tank after t minute.
amount of salt in the tank after t minute.