Question

1. A 2.5 kg led projector is launched as a projectile off a tall building. At one point, as it

is flying through the air it has a velocity of 24 m/s and a height of 14 m.
a) Find the potential energy
b) Find the kinetic energy
c) Find the total mechanical energy
d) Find the potential energy at a height of 8.7 m
e) Find the kinetic energy at that same height. (Hint – the total energy is always the same
as in part c)
f) Find the velocity at that height
g) Find the velocity at a height of 11.6 m
h) At what height would the velocity be 26 m/s?
i) What is the velocity just before it smashes into the ground?
See

Answer 1

Step-by-step explanation:

I got everything but i. Don't know why but it's eluding me. So let's do everything but that.

a. PE = mgh so

PE = (2.5)(98)(14) and

PE = 340 J

b.
`KE=(1)/(2)mv^2` so

`KE=(1)/(2)(2.5)(14)^2` and

KE = 250 J

c. TE = KE + PE so

TE = 340 + 250 and

TE = 590 J

d. PE at 8.7 m:

PE = (2.5)(9.8)(8.7) and

PE = 210 J

e. The KE at the same height:

TE = KE + PE and

590 = KE + 210 so

KE = 380 J

f. The velocity at that height:

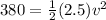`380=(1)/(2)(2.5)v^2` and

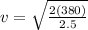`v=\sqrt{(2(380))/(2.5) }` so

v = 17 m/s

g. The velocity at a height of 11.6 m (these get a bit more involed as we move forward!). First we need to find the PE at that height and then use it in the TE equation to solve for KE, then use the value for KE in the KE equation to solve for velocity:

590 = KE + PE and

PE = (2.5)(9.8)(11.6) so

PE = 280 then

590 = KE + 280 so

KE = 310 then

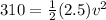`310=(1)/(2)(2.5)v^2` and

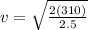`v=\sqrt{(2(310))/(2.5) }` so

v = 16 m/s

h. This one is a one-dimensional problem not using the TE. This one uses parabolic motion equations. We know that the initial velocity of this object was 0 since it started from the launcher. That allows us to find the time at which the object was at a velocity of 26 m/s. Let's do that first:

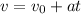`v=v_0+at` and

26 = 0 + 9.8t and

26 = 9.8t so the time at 26 m/s is

t = 2.7 seconds. Now we use that in the equation for displacement:

Δx =
`v_0t+(1)/(2)at^2` and filling in the time the object was at 26 m/s:

Δx = 0t +
`(1)/(2)(-9.8)2.7)^2` so

Δx = 36 m

i. ??? In order to find the velocity at which the object hits the ground we would need to know the initial height so we could find the time it takes to hit the ground, and then from there, sub all that in to find final velocity. In my estimations, we have 2 unknowns and I can't seem to see my way around that connundrum.