Answer:
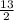
Explanation:
slope of the line that passes thru (5, 3) and (8, A)

the line that is perpendicular to the given line is
6x + 7y + 13= 0
finding the slop of this line :-
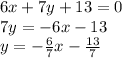
Comparing with standard equation of a line
y = mx + c
- where m is the slop and c is the y- intercept
m = - 6/ 7
Since, the two lines are perpendicular to each other the product of their slopes will be - 1
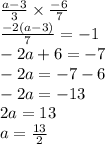
( canceling the 2 negative signs on both the sides )