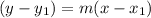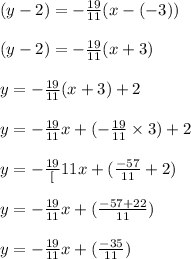Answer:

Explanation:
Find intersection of the given lines :
x - 2y = 0 => x = 2y ----------- ( 1 )
3x + y = - 5 -------------------- ( 2 )
Substitute ( 1 ) in ( 2 ) :
3x + y = - 5
3 ( 2y ) + y = - 5
6y + y = - 5
7y = - 5
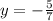
Substitute y in ( 1 ) :
x = 2y
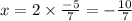
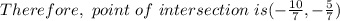
To find the equation of the line passing through ( - 3, 2) and point of intersection :
Standard equation of a line : y = mx + b , where m is the slope, b is the y intercept.
So step 1 : Find slope , m:
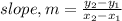
![[ \ where \ (x_1, y_ 1 ) = ( -3, 2 ) \ and \ (x_2, y_ 2 ) = ( (-10)/(7) , (-5)/(7)) \ ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/962vbx5tjmueu2r5arevipras82gecx3rm.png)

Step 2 : Equation of the line :