Question

The equation x ^ 2 - 2x + y ^ 2 - 4y = 20 defines a circle in the xy-coordinate plane What is the radius of the circle?

Answer 1

I'll set up the problem and you can do the calculation

Explanation:

we need to complete the squares to get the equation in the general form:

`{(x - h)}^(2) + {(y - k) }^(2) = {r}^(2)`

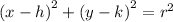
where h = the x coordinate of the center

k = the y coordinate of the center

r = the radius

so looking at

`{x}^(2) - 2x`

we can see that if use -1 as the constant we have

`{(x - 1)}^(2) = {x}^(2) - 2x + 1`

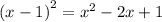
doing the same for y

`{y}^(2) - 4y`

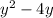
we can use -2 as the constant (basically you that the s

quare of the y coefficient )

`{(y - 2)}^(2) = {y}^(2) - 4y + 4`

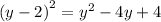
so now we have to add or subtract the constant on the RHS to see what the square of the radius is according to the general form of the equation at the top

20 +1+4=25

Take the square root and you have the radius