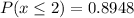Answer:
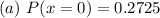
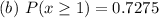
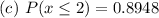
Explanation:
Given
 --- 8 friends
--- 8 friends
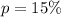 --- proportion that one-time fling
--- proportion that one-time fling
This question is an illustration of binomial probability, and it is represented as:
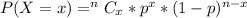
Solving (a): P(x = 0) --- None has done one time fling
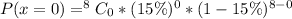
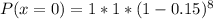
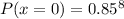
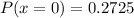
Solving (b):
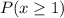
To do this, we make use of compliment rule:
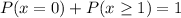
Rewrite as:
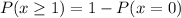
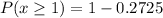
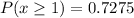
Solving (c):
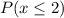 --- Not more than 2 has one time fling
--- Not more than 2 has one time fling
This is calculated as:

We have:
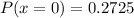
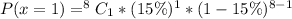
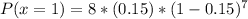

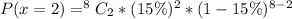
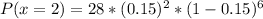
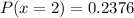
So: