Answer:
the calculated ratio to the radius of the sodium
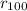 /
/
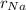 is 2645.0
is 2645.0
Step-by-step explanation:
Given the data in the question;
the calculated ratio to the radius of the sodium =
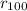 /
/
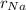
so from here we can write the number of energy states as 100
The number of energy states; n = 100
A;
We know that the radius of the sodium atom is;
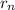 = n²α₀
= n²α₀
Now, the value of the Bohr radius; α₀ = 5.29 × 10⁻¹¹ m
so lets determine the radius of the sodium atom; by substituting in our values;
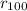 = (100)² × (5.29 × 10⁻¹¹ m )
= (100)² × (5.29 × 10⁻¹¹ m )
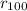 = 5.29 × 10⁻⁷ m
= 5.29 × 10⁻⁷ m
B
given that, the theoretical value of the radius of the sodium is;
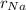 = 0.2 nm = 2 × 10⁻¹⁰ m
= 0.2 nm = 2 × 10⁻¹⁰ m
so we calculate the ratio of the radii of the sodium;
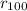 /
/
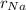 = ( 5.29 × 10⁻⁷ m ) / ( 2 × 10⁻¹⁰ m )
= ( 5.29 × 10⁻⁷ m ) / ( 2 × 10⁻¹⁰ m )
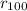 /
/
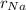 = 2645.0
= 2645.0
Therefore, the calculated ratio to the radius of the sodium
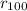 /
/
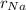 is 2645.0
is 2645.0