Answer:
Approximately
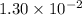 , assuming that this acid is monoprotic.
, assuming that this acid is monoprotic.
Step-by-step explanation:
Assume that this acid is monoprotic. Let
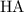 denote this acid.
denote this acid.
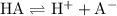 .
.
Initial concentration of
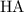 without any dissociation:
without any dissociation:
![[{\rm HA}] = 0.730\; \rm mol \cdot L^(-1)](https://img.qammunity.org/2022/formulas/chemistry/college/dp4ze739t1ktun2l039smnpl0ljvpkj7n6.png) .
.
After
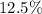 of that was dissociated, the concentration of both
of that was dissociated, the concentration of both
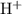 and
and
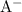 (conjugate base of this acid) would become:
(conjugate base of this acid) would become:
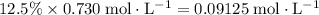 .
.
Concentration of
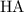 in the solution after dissociation:
in the solution after dissociation:
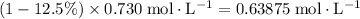 .
.
Let
![[{\rm HA}]](https://img.qammunity.org/2022/formulas/chemistry/college/odbrd5k6xx6hicb9sbib4470dy28rioxqw.png) ,
,
![[{\rm H}^(+)]](https://img.qammunity.org/2022/formulas/chemistry/college/83jbcjopbi0htj6o6taoodrupzd9a4pglq.png) , and
, and
![[{\rm A}^(-)]](https://img.qammunity.org/2022/formulas/chemistry/college/4kgez17nffmevuqekd7ltd8vc3gxipvnoz.png) denote the concentration (in
denote the concentration (in
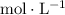 or
or
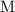 ) of the corresponding species at equilibrium. Calculate the acid dissociation constant
) of the corresponding species at equilibrium. Calculate the acid dissociation constant
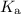 for
for
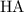 , under the assumption that this acid is monoprotic:
, under the assumption that this acid is monoprotic:
![\begin{aligned}K_(\rm a) &= \frac{[{\rm H}^(+)] \cdot [{\rm A}^(-)]}{[{\rm HA}]} \\ &= ((0.09125\; \rm mol \cdot L^(-1)) * (0.09125\; \rm mol \cdot L^(-1)))/(0.63875\; \rm mol \cdot L^(-1))\\[0.5em]&\approx 1.30 * 10^(-2) \end{aligned}](https://img.qammunity.org/2022/formulas/chemistry/college/t2w7n8qgn9eif5n1sxor0oq5cxsesn0hyv.png) .
.