1 Answer

Nephewtom · Answer 1 · 2022-03-25T10:25:03+0000

Given:

One of two complementary angles is 35º larger than the other.

To find:

The measure of both angles.

Solution:

Let x degrees be the measure of smaller angle. Then the measure of larger angle is:

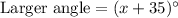
$\text{Larger angle}=(x+35)^\circ$

We know that the sum of complimentary angles is always 90 degrees. So,

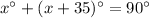
$x^\circ+(x+35)^\circ=90^\circ$

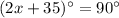
$(2x+35)^\circ=90^\circ$

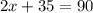
2x+35=90

Subtract 35 from both sides.

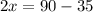
2x=90-35

2x=55

x=(55)/(2)

x=27.5

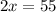
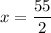
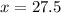
The measure of smaller angle is 27.5 degrees.

Now, the measure of larger angle is:

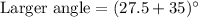
$\text{Larger angle}=(27.5+35)^\circ$

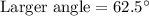
$\text{Larger angle}=62.5^\circ$

Therefore, the measures of both angles are 27.5° and 62.5°.

Please log in or register to add a comment.