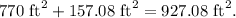Question

The patio at the back of the house is to be extended into the backyard in a semi-circle. What will be the area of the yard

after the patio is done?

Answer 1

The area of the yard is 927 square ft.

To calculate the area of the yard after the patio is extended into the backyard in a semi-circle, we need to calculate the area of the semi-circular extension and then add it to the area of the rectangular part of the yard.

Here's how to do it:

1. Calculate the area of the rectangle: Multiply the length by the width of the rectangular part of the yard.

2. Calculate the area of the full circle: Use the formula
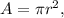`\( A = \pi r^2 \),`where r is the radius of the circle. Since we only have a semi-circle (half of a full circle), we will divide this area by 2.

3. Add the two areas together: Sum the area of the rectangle and the semi-circle to get the total area.

Let's start by calculating the area of the rectangular part of the yard:

Given dimensions:

- Width (across the semi-circle) = 20 ft

- Length (height of the rectangle) = 38.5 ft (since 1/2 ft is equal to 6 inches)

The radius of the semi-circle will be half of the width of the rectangle, which is 10 ft.

Now we'll perform the calculations to find the total area.

The total area of the yard after the patio is extended into the backyard in a semi-circle is approximately 927.08 square feet when rounded to two decimal places.

Here are the detailed steps:

1. The area of the rectangular part of the yard is
`\(20 \text{ ft} * 38.5 \text{ ft} = 770 \text{ ft}^2\).`

2. The area of the full circle would be
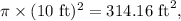`\( \pi * (10 \text{ ft})^2 = 314.16 \text{ ft}^2\),`and therefore the area of the semi-circle is half of that, which is
`\( (314.16)/(2) \text{ ft}^2 \approx 157.08 \text{ ft}^2\).`

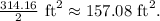
3. Adding the areas of the rectangle and the semi-circle together gives
`\( 770 \text{ ft}^2 + 157.08 \text{ ft}^2 = 927.08 \text{ ft}^2\).`

Answer 2

A = 413 sq feet

Explanation:

The area of the yard = area of rectangle - area of semicircle

The radius of the semicircle, r = 10 feet

The length of the rectangle = 38.5 - 10 = 28.5 feet

So,

The area of the yard = lb - (πr²/2)

`=20* 28.5-((3.14* 10^2)/(2))\\\\A=413\ ft^2`

So, the required area is equal to 413 sq feet.