Question

I need to match them but I don't know how

Answer 1

Given:

The system of equations is:

`x+3y=5`

`x-3y=-1`

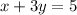
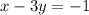
The given matrices are
`\left[\begin{array}{cc}5&3\\-1&-3\end{array}\right]`,
`\left[\begin{array}{cc}1&5\\1&-1\end{array}\right]`,
`\left[\begin{array}{cc}1&3\\1&-3\end{array}\right]`.

To find:

The correct names for the given matrices.

Solution:

We have,

`x+3y=5`

`x-3y=-1`

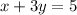
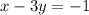
Here, coefficients of x are 1 and 1 respectively, the coefficients of y are 3 and -3 respectively and constant terms are 5 and -1 respectively.

In the x-determinant, the coefficients of x are in the first column and the constant terms are in the second column. So, the x-determinant is:

`\left[\begin{array}{cc}1&5\\1&-1\end{array}\right]`

In the y-determinant, the constant terms are in the first column and the coefficients of y are in the second column. So, the y-determinant is:

`\left[\begin{array}{cc}5&3\\-1&-3\end{array}\right]`

In the system determinant, the coefficients of x are in the first column and the coefficients of y are in the second column. So, the system determinant is:

`\left[\begin{array}{cc}1&3\\1&-3\end{array}\right]`

Therefore, the first matrix is y-determinant, second matrix is x-determinant and the third matrix is the system determinant.