Question

Consider the following graph:

What is the limit as it is approaching -1 from the right, what is the limit?

Answer 1

The limit
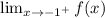`\(\lim_{{x \to -1^+}} f(x)\)` for the given graph of y = f(x) is 0. As x approaches -1 from the right, f(x) tends to 0, as indicated by the graph's behavior.

The given description of the graph provides information about the behavior of f(x) near x = -1. The notation
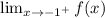`\(\lim_{{x \to -1^+}} f(x)\)` represents the limit as x approaches -1 from the right.

From the description:

1. The curve starts at (-3,2) and ends at (-1,2). This indicates that as x approaches -1 from the right, f(x) approaches 2.

2. Another curve starts at (-1,0), passes through (0,1), (1,0), and ends between 1 and 2 on the x-axis. This indicates that as x approaches -1 from the right, f(x) approaches 0.

Therefore,
`\(\lim_{{x \to -1^+}} f(x) = 0\).`

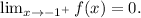
Answer: e. 0

This is because as x approaches -1 from the right, f(x) approaches 0 according to the described graph behavior.

Answer 2

The limit is 0, and the answer is given by option E.

Explanation:

Limit to the right:

The limit of a function approacing a value of x to the right is given by the value of the function quite close to the point, looking to the right.

In this question:

Approacing by the right(x quite close, but more than -1, that is, -0.9999...), y tends to 0, so the limit is 0, and the answer is given by option E.