Question

What is the inverse of the function f(x) = 4x^3 - 9

Answer 1

`f(x)^-^1=\sqrt[3]{(x+9)/(4)}`

Explanation:

Finding the inverse of a function is essentially doing a given function in backwards order. An easy trick to doing such is to treat the evaluation (f(x)) like a variable. Think of the function as an equation, then solve the function for (x) in terms of (f(x)).

`f(x)=4x^3-9`

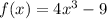
Inverse operations,

`f(x)=4x^3-9\\\\(f(x))+9=4x^3\\\\(((f(x))+9))/(4)=x^3\\\\\sqrt[3]{((f(x))+9)/(4)}=x`

Now put this in the form of an inverse function, switch the places of the terms (x) and (f(x)), remember to indicate that it is an inverse function,

`f(x)^-^1=\sqrt[3]{(x+9)/(4)}`