Answer:
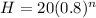
Explanation:
So, lets just go over this step by step and make sense of it.
20 clearly must be what we start with, and as you see in your answers, all of them have that as the number you multiply the parethese by.
Its what next that we dont know about.
We know that the ball rebounds 80% of its previous height.
It for sure cannot be a or d because a would mean that it would only rebound 20% of its height, and d would mean that it rebound 180% of its height.
Its now between b and c.
Lets just think about it.
Pull out your calculator or pull it up on your electronic. Multiply 10 by 0.9. This will get you 9. Multiply 9 again by 0.9, and youll get 8.1.
What did we actually do there? We did 10*0.9^2
Pull out your calculator again and try 10* 0.9^2. Youll see that 0.9 squared is 0.81. This times 10 is 8.1, and that is exactly what you got before.
Understanding this, it is clear that we must use an exponent to fidn future values.
In answer b, it shows that you can just multiply by n.
In answer c however, it uses n as an exponent, which is the correct thing to do.
So c is your answer.
The actual formula for this is:

The first term in this case is the first height, which is 20. The change is a rebound of 80%(0.8).
The term is just n, but in most problems n is time.
Hope this helps!