Question

Hey!! Can anyone PLZ help the picture is down below .Thank you!!

Answer 1

`\huge\bold{Given :}`

Angle CBA = 60°

Angle BAC = 40°

Angle BCA =
`x`

`\huge\bold{To\:find :}`

The measure of angle
`x`.

`\large\mathfrak{{\pmb{\underline{\orange{Solution}}{\orange{:}}}}}`

`\implies {\blue {\boxed {\boxed {\purple {\sf {x\:=\:80°}}}}}}`

`\large\mathfrak{{\pmb{\underline{\red{Step-by-step\:explanation}}{\red{:}}}}}`

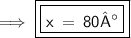
We know that,

`\sf\pink{Sum\:of\:angles\:of\:a\:triangle\:=\:180°}`

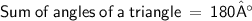
➪ ∠ CBA + ∠ BAC + ∠ BCA = 180°

➪ 60° + 40° +
`x` = 180°

➪ 100° +
`x` = 180°

➪
`x` = 180° - 100°

➪
`x` = 80°

Therefore, the measure of angle
`x` is 80°.

Now, the three angles of the triangle are 60°, 40° and 80° respectively.

`\large\mathfrak{{\pmb{\underline{\blue{To\:verify}}{\blue{:}}}}}`

∠ CBA + ∠ BAC + ∠ BCA = 180°

✒ 60° + 40° + 80° = 180°

✒ 180° = 180°

✒ L. H. S. = R. H. S.

`\boxed{Hence\:verified.}`

`\huge{\textbf{\textsf{{\orange{My}}{\blue{st}}{\pink{iq}}{\purple{ue}}{\red{35}}{\green{ヅ}}}}}`