Question

Simplify the following expression using imaginary numbers. Express your answer in a + bi form

i^80+i^38-i17 please show work

Answer 1

0 - 17i

Explanation:

Given expression;

i⁸⁰ + i³⁸ - i17

To express the expression in the form a+bi;

i. Rewrite the expression such that it contains terms in i²

(i²)⁴⁰ + (i²)¹⁹ - i17

ii. Solve the result from (i) above using the identity i² = -1

We know that the square root of -1 is i. i.e

`√(-1) = i`

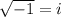
Squaring both sides gives

=>
`(√(-1) )^(2) = i^(2)`

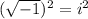
=> -1 = i²

Therefore,

i² = -1

Substitute i² = -1 in step (i) above

(-1)⁴⁰ + (-1)¹⁹ - i17

(iii) Solve the result in (ii)

We know that the when a negative number is raised to the power of an even number, the result is a positive number. If it is raised to the power of an odd number, the result is a negative number. Therefore,

(-1)⁴⁰ + (-1)¹⁹ - i17 becomes

1 + (-1) - i17

0 - i17

(iv) Write the result from (iii) in the form a+bi

0 - 17i