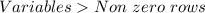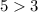Question

Determine by inspection (i.e., without performing any calculations) whether a linear system with the given augmented matrix has a unique solution, infinitely many solutions, or no solution. 1 2 3 4 5 6 7 6 5 4 3 2 8 8 8 8 8 8

Answer 1

Infinitely Many Solutions

Explanation:

Given

`\left[\begin{array}{cccccc}1&2&3&4&5&6\\7&6&5&4&3&2\\8&8&8&8&8&8\end{array}\right]`

Required

Determine the type of solution

From the matrix, we have:

3 non-zero rows and 5 variables (the last column is the result)

When the number of variables is more than the number of non-zero rows, then such system has infinitely many solutions

i.e.

`Variables > Non\ zero\ rows`

`5 > 3`