Question

Question 2 of 27

A man is trying to drag a small tree that he cut down. If the static coefficient
of friction of the tree on the ground is 0.5 and the tree weighs 670 N, what is
the minimum amount of horizontal force that the man will need to apply so
that the tree will start moving?
A. 670 N
B. 230 N
C. 335 N
D. 465 N

Answer 1

Step-by-step explanation:

Newton's 2nd Law say that F = ma which is the sum of the forces acting on an object is equal to the object's mass times the acceleration at which it is moving. That means that the forces acting on this tree are F which is the Force the man needs to exert to move the tree, and f which is the force the tree is exerting in an effort to stay right where it is. That alters our 2nd Law equation to F - f = ma. BUT if the tree isn't moving, the acceleration is 0, making the whole right side of that equation go to 0. That means that F = f. Phew! Let's do that.

f = μ
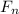`F_n` where f is the frictional force, μ is the coefficient of static friction, and
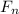`F_n` is the weight of the object, which are given as 670 N. Filling in:

f = .5(670) so

f = 335 N (that is not using the rules of significant digits properly, but if you use them properly, the answer is not one of the choices, so...)

C is the one you want.