Question

In the figure below, what is the value of xº?

68
100°

A. 800
B. 689
C. 32°
D. 180°

Answer 1

`\huge\bold{Given :}`

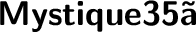
Angle AOB = 100°

Angle OBC = 68°

Angle BCO =
`x°`

`\huge\bold{To\:find :}`

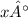
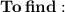
The value of
`x°`.

`\large\mathfrak{{\pmb{\underline{\orange{Solution}}{\orange{:}}}}}`

`\implies {\blue {\boxed {\boxed {\purple {\sf {C.\:x°\:=\:32°}}}}}}`

`\large\mathfrak{{\pmb{\underline{\red{Step-by-step\:explanation}}{\red{:}}}}}`

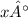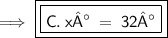
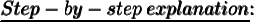
An exterior angle of a triangle is equal to sum of two opposite interior angles.

And so we have,

➪ ∠ AOB = ∠ OBC + ∠ BCO

➪ 100° = 68° +
`x°`

➪
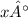`x°` = 100° - 68°

➪
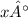`x°` = 32°

Therefore, the value of
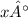`x°` is 32°.

`\large\mathfrak{{\pmb{\underline{\blue{To\:verify}}{\blue{:}}}}}`

∠ AOB = ∠ OBC + ∠ BCO

✒ 100° = 68° + 32°

✒ 180° = 100°

✒ L. H. S. = R. H. S.

`\boxed{Hence\:verified.}`

(Note: Kindly refer to the attached file.)

`\huge{\textbf{\textsf{{\orange{My}}{\blue{st}}{\pink{iq}}{\purple{ue}}{\red{35}}{\green{ヅ}}}}}`

Answer 2

x = 32

Explanation:

The exterior angle of a triangle is equal to the sum of the opposite interior angles

100 = 68+x

Subtract 68 from each side

100 -68 = x

32 =x