Question

A line passes through (3, -2) and (6, 2).

a. Write an equation for the line in point-slope form.
b. Rewrite the equation in standard form using integers.

Answer 1

Explanation:

Point-slope form implies that we need the slope. Let's find that first. Point-slope form, btw, is
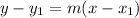`y-y_1=m(x-x_1)`, and the formula to find slope is

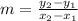`m=(y_2-y_1)/(x_2-x_1)` so filling in:

`m=(2-(-2))/(6-3)=(4)/(3)` so the slope is a fraction. No problem. It looks the point (3, -2) was used to write the line, so the line in point-slope form using that point is

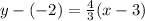`y-(-2)=(4)/(3)(x-3)` which simplifies a bit to

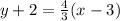`y+2=(4)/(3)(x-3)`. Rewriting in standard form using integers means that we get x and y on the same side of the equals sign, and no fractions allowed. Begin by distributing through the parenthesis to get

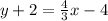`y+2=(4)/(3)x-4` and get rid of the 3 in the denominator by multiplying everything by 3:

3y + 6 = 4x - 12. Now get the x and y on the same side and the constants on the other side.

-4x + 3y = -18. The choice you want is the first one.