Answer:
64
 in²
in²
Explanation:
I did not ever do a problem like this, however this is the beauty of math, you can easily reverse engineer it.
Remember,
A =

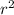
And if we have 4 circles that means the area of one circle is 1/4th the total
So,
A=
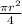
Assuming that 16 is the radius squared times 4 lets ignore that squared for now because when going backwards we would get rid of the squared last as that was the first step.
A=
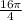 =
=
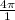 =4
=4

Now lets get it back to
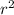 by square rooting the 4
by square rooting the 4
A=
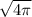 =2
=2

The radius of one small circle is 2. Therefore; the diameter would be 4 for each. This in mind we know that two small circles diameters make up the radius of the larger circle we will multiply it by two again.
This gives us a final radius of the bigger circle of 8
Therefore, the area of the bigger circle is 8²
 which simplifies to 64
which simplifies to 64

And a final answer of
64
 in²
in²
Hope this helps :)