Question

A gymnast is swinging on a high bar. The distance between his waist and the bar is 1.06 m, as the drawing shows. At the top of the swing his speed is momentarily zero. Ignoring friction and treating the gymnast as if all of his mass is located at his waist, find his speed at the bottom of the swing.

Answer 1

Answer: The speed of gymnast at the bottom of the swing is 6.44 m/s.

Step-by-step explanation:

Given: Distance = 1.06 m

According to the law of conservation of energy, the speed is calculated as follows.

`mgh = - mgh + (1)/(2)mv^(2)\\gh = - gh + (1)/(2)v^(2)\\v = √(4gh)`

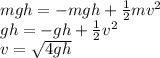
where,

g = acceleration due to gravity = 9.8
`m/s^(2)`

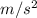
h = distance

v = speed

Substitute the values into above formula as follows.

`v = √(4gh)\\= \sqrt{4 * 9.8 m/s^(2) * 1.06}\\= 6.44 m/s`

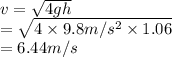
Thus, we can conclude that speed of gymnast at the bottom of the swing is 6.44 m/s.