This question is incomplete, the complete question is;
A manufacturing facility with a wastewater flow of 0.011 m³/sec and a BOD₅ of 590 mg/L discharges into the Cattaraugus Creek. The creek has a 10-year, 7-day low flow of 1.7 m³/sec. Upstream of the facility, the BOD₅ of the creek is 0.6 mg/L. The BOD rate constants k are 0.115 d⁻¹ for the wastewater and 3.7 d⁻¹ for the creek. The temperature of both the creek and tannery of wastewater is 20°C. Determine: [A] UBOD of wastewater. [B] UBOD of creek. [C] What is the initial ultimate BOD after mixing
Answer:
a) Ultimate BOD of wastewater is 1349.188 mg/L
b) Ultimate BOD of creek is 0.6 mg/L
c) the initial ultimate BOD after mixing is 9.27 mg/L
Step-by-step explanation:
Given the data in the question;
Q
 = 0.011 m³/s
= 0.011 m³/s
BOD
 = 590 mg/L
= 590 mg/L
Q
 = 1.7 m³/sec
= 1.7 m³/sec
BOD
 = 0.6 mg/L
= 0.6 mg/L
time t = 5
rate constants k for wastewater = 0.115 d⁻¹
rate constants k for creek = 3.7 d⁻¹
a) UBOD of wastewater.
The Ultimate BOD of wastewater is;
BOD
 = L₀
= L₀
 ( 1 -
( 1 -
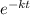 )
)
where BOD
 is the BOD of wastewater after 5 days, L₀
is the BOD of wastewater after 5 days, L₀
 is the ultimate BOD of wastewater, k is the rate constant of wastewater and t is the time( days ).
is the ultimate BOD of wastewater, k is the rate constant of wastewater and t is the time( days ).
we make L₀
 the subject of formula
the subject of formula
BOD
 = L₀
= L₀
 ( 1 -
( 1 -
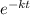 )
)
L₀
 = BOD
= BOD
 / ( 1 -
/ ( 1 -
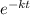 )
)
so we substitute
L₀
 = 590 / ( 1 -
= 590 / ( 1 -
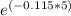 )
)
L₀
 = 590 / ( 1 -
= 590 / ( 1 -
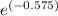 )
)
L₀
 = 590 / ( 1 - 0.5627 )
= 590 / ( 1 - 0.5627 )
L₀
 = 590 / 0.4373
= 590 / 0.4373
L₀
 = 1349.188 mg/L
= 1349.188 mg/L
Therefore, Ultimate BOD of wastewater is 1349.188 mg/L
b) UBOD of creek
The Ultimate BOD of creek is;
BOD
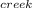 = L₀
= L₀
 ( 1 -
( 1 -
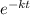 )
)
we make L₀
 the subject of formula
the subject of formula
L₀
 = BOD
= BOD
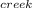 / (1 -
/ (1 -
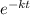 )
)
we substitute
L₀
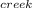 = 0.6 / ( 1 -
= 0.6 / ( 1 -
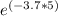 )
)
L₀
 = 0.6 / ( 1 -
= 0.6 / ( 1 -
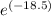 )
)
L₀
 = 0.6 / ( 1 - (9.2374 × 10⁻⁹) )
= 0.6 / ( 1 - (9.2374 × 10⁻⁹) )
L₀
 = 0.6 / 0.99999
= 0.6 / 0.99999
L₀
 = 0.6 mg/L
= 0.6 mg/L
Therefore, Ultimate BOD of creek is 0.6 mg/L
c) the initial ultimate BOD after mixing;
Lₐ = [( Q
 × L₀
× L₀
 ) + ( Q
) + ( Q
 × L₀
× L₀
 )] / [ Q
)] / [ Q
 + Q
+ Q
 ]
]
we substitute
Lₐ = [( 0.011 × 1349.188 ) + ( 1.7 × 0.6 )] / [ 0.011 + 1.7 ]
Lₐ = [ 14.841068 + 1.02 ] / 1.711
Lₐ = 15.861068 / 1.711
La = 9.27 mg/L
Therefore, the initial ultimate BOD after mixing is 9.27 mg/L