Question

A 62.0 kg water skier at rest jumps from the dock into a 775 kg boat at rest on the east side of the dock. If the velocity of the skier is 4.50 m/s as she leaves the dock, what is the final velocity of the skier and boat?

2.78 m/s to the east
2.78 m/s to the west
0.360 to the west
0.360 to the east

Answer 1

The final velocity of the skier and boat is 0.33 m/s to the east.

Step-by-step explanation:

We can find the final velocity of the skier by conservation of linear momentum:

`m_(s)v_{s_(i)} + m_(b)v_{b_(i)} = m_(s)v_{s_(f)} + m_(b)v_{b_(f)}`

Where:

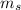`m_(s)`: is the mass of the water skier = 62.0 kg

`m_(b)`: is the mass of the boat = 775 kg

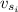`v_{s_(i)}`: is the initial velocity of the skier = 4.50 m/s (as she leaves the dock)

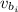`v_{b_(i)}`: is the initial velocity of the boat = 0 (it is at rest)

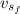`v_{s_(f)}`: is the final velocity of the skier =?

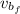`v_{b_(f)}`: is the final velocity of the boat =?

Since the final velocity of the skier is the same that the velocity of the boat (
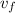`v_(f)`) we have:

`m_(s)v_{s_(i)} + 0 = v_(f)(m_(s) + m_(b))`

[tex]v_{f} = \frac{m_{s}v_{s_{i}}}{m_{s} + m_{b}} = \frac{62.0 kg*4.50 m/s}{62.0 kg + 775 kg} = 0.33 m/s

Therefore, the final velocity of the skier and boat is 0.33 m/s to the east.

I hope it helps you!