Question

A study shows that 20% of college students pray daily in their own religious beliefs. In a group of 300 college students, find the probability that 57 to 62 of them pray daily in their own religious beliefs. Use up to 4 decimal places accuracy for

μ
ˆ
p
,
σ
ˆ
p
, and your answer.

0.2805
0.6141
0.47385
0.3336
None of the above.

Answer 1

0.2805

Explanation:

Given that p = 20% = 0.2, n = 300.

The mean (μ) = np = 0.2 * 300 = 60

The standard deviation (σ) =
`√(np(1-p))=√(300*0.2(1-0.2))=6.93`

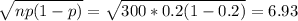
The z score is used to determine by how many standard deviations the raw score is above or below the mean. The z score is given by:

`z=(x-\mu)/(\sigma )`

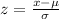
For x = 57:

`z=(57-60)/(6.93 ) =-0.43`

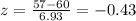
For x = 62:

`z=(62-60)/(6.93 ) =0.29`

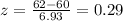
From the normal distribution table, P(57 < x < 62) = P(-0.43 < z < 0.29) = P(z < 0.29) - P(z < -0.43) = 0.6141 - 0.3336 = 0.2805