Question

The probability that a male professional golfer makes a hole-in-one is 1/2780. Suppose 36 professional male golfers play the sixth hole during a round of golf. Let the random variable X be the number of golfers in the group of 36 who make a hole-in-one. Calculate the probability that exactly four of the 36 golfers make a hole-in-one on the sixth hole – as actually happened during the 1989 U.S. Open

Answer 1

The right solution is "
`9.7* 10^(-10)`".

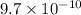Explanation:

According to the question,

The probability that male professional golfer makes hole in one will be:

`P=(1)/(2780)`

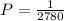
Number of players,

n = 36

and,

`q=1-P=(2779)/(2780)`

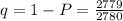
By using the Binomial theorem, we get

⇒
`P(x=r) = \binom{n}{r} p^r q^(n-r)`

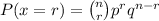
Bu substituting the values, we get

`=\binom{36}{4} ((1)/(2780) )^4 ((2779)/(2780) )^(32)`

`=9.74929* 10^(-10)`

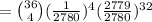
or,

`=9.7* 10^(-10)`