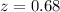Answer:
The value of the z-test statistic is
Explanation:
An article claims that 12% of trees are infested by a bark beetle.
At the null hypothesis, we test if the proportion is of 12%, that is:

At the alternative hypothesis, we test if the proportion is different of 12%, that is:
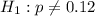
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
0.12 is tested at the null hypothesis:
This means that
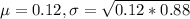
A random sample of 1,000 trees were tested for traces of the infestation and found that 127 trees were affected.
This means that
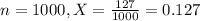
What is the value of the z-test statistic?


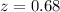
The value of the z-test statistic is