And

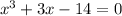
➺
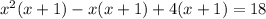
➺
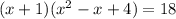
➺
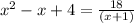
➺
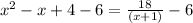
➺
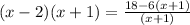
➺
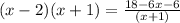
➺
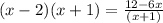
➺
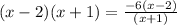
➺
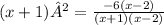
➺
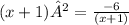
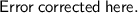
➺
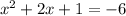
➺
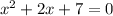
By quadratic formula, we have
➺
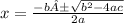
➺
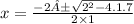
➺
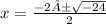
➺
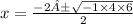
➺
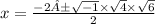
➺
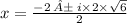
➺
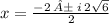
➺
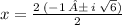
➺
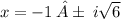
Therefore, the two values of
 are (
are (
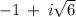 ) and (
) and (
 ).
).
Let us look at another method.
 ³ + 3
³ + 3
 - 14 = 0
- 14 = 0
➼
 ³ + 3
³ + 3
 = 14
= 14
➼
 (
(
 ² + 3 ) = 14
² + 3 ) = 14
Factors of 14 = 1, 2, 7 and 14.
a) Substituting
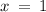 , we have
, we have
➼ 1 ( 1 + 3 ) ≠ 14
➼ 1 x 4 ≠ 14
➼
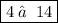
b) Substituting
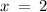 , we have
, we have
➼ 2 ( 2² + 3 ) = 14
➼ 2 ( 4 + 3 ) = 14
➼ 2 x 7 = 14
➼

c) Substituting
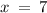 , we have
, we have
➼ 7 ( 7² + 3 ) ≠ 14
➼ 7 ( 49 + 3 ) ≠ 14
➼ 7 x 52 ≠ 14
➼
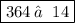
d) Substituting
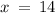 , we have
, we have
➼ 14 ( 14² + 3 ) ≠ 14
➼ 14 x 199 ≠ 14
➼
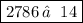
Hence, our only real solution is 2.