Question

A baseball is hit and its height at different one-second intervals is recorded (See attachment)

Answer 1

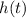`h(t)` is likely a quadratic function.

Based on values in the table, domain of
`h(t)` :
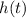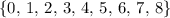`\lbrace 0,\, 1,\, 2,\, 3,\, 4,\, 5,\, 6,\, 7,\, 8\rbrace`; range of
`h(t)\!`:
`\lbrace 0,\, 35.1,\, 60.1\, 75.2,\, 80.3,\, 75.3,\, 60.2,\, 35.0 \rbrace`.

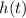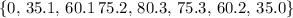Explanation:

By the power rule,
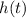`h(t)` is a quadratic function if and only if its first derivative,
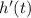`h^\prime(t)`, is linear.

In other words,
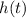`h(t)` is quadratic if and only if
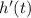`h^\prime(t)` is of the form
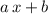`a\, x + b` for some constants
`a` and
`b`. Tables of differences of
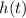`h(t)\!` could help approximate whether
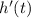`h^\prime(t)\!` is indeed linear.

Make sure that values of
`t` in the first row of the table are equally spaced. Calculate the change in
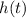`h(t)` over each interval:

• 
  `h(1) - h(0) = 35.1`.
• 
  `h(2) - h(1) = 25.0`.
• 
  `h(3) - h(2) = 15.1`.
• 
  `h(4) - h(3) = 5.1`.
• 
  `h(5) - h(4) = -5.0`.
• 
  `h(6) - h(5) = -15.1`.
• 
  `h(7) - h(6) = -25.2`.
• 
  `h(8) - h(7) = -35.0`.

Consecutive changes to the value of
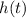`h(t)` appears to resemble a line with slope
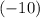`(-10)` within a margin of
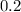`0.2`. Hence, it is likely that
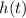`h(t)\!` is indeed a quadratic function of
`t`.

The domain of a function is the set of input values that it accepts. For the
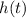`h(t)` of this question, the domain of
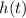`h(t)\!` is the set of values that
`t` could take. These are listed in the first row of this table.

On the other hand, the range of a function is the set of values that it outputs. For the
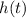`h(t)` of this question, these are the values in the second row of the table.

Since both the domain and range of a function are sets, their members are supposed to be unique. For example, the number "
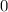`0`" appears twice in the second row of this table: one for
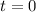`t = 0` and the other for
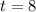`t = 8`. However, since the range of
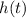`h(t)` is a set, it should include the number
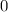`0\!` only once.