Answer:
c. 36·x
Explanation:
Part A
The details of the circle are;
The area of the circle, A = 12·π cm²
The diameter of the circle, d =

Given that
 is the diameter of the circle, we have;
is the diameter of the circle, we have;
The length of the arc AB = Half the the length of the circumference of the circle
Therefore, we have;
A = 12·π = π·d²/4 = π·
 ²/4
²/4
Therefore;
12 =
 ²/4
²/4
4 × 12 =
 ²
²
 ² = 48
² = 48
 = √48 = 4·√3
= √48 = 4·√3
 = 4·√3
= 4·√3
The circumference of the circle, C = π·d = π·

Arc AB = Half the the length of the circumference of the circle = C/2
Arc AB = C/2 = π·
 /2
/2
 = 4·√3
= 4·√3
∴ C/2 = π·4·√3/2 = 2·√3·π
The length of arc AB = 2·√3·π cm
Part B
The given parameters are;
The length of
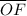 = The length of
= The length of
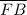
Angle D = angle B
The radius of the circle = 6·x
The measure of arc EF = 60°
The required information = The perimeter of triangle DOB
We have;
Given that the base angles of the triangles DOB are equal, we have that ΔDOB is an isosceles triangle, therefore;
The length of
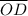 = The length of
= The length of

The length of
 =
=
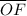 +
+
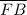 =
=
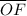 +
+
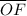 = 2 ×
= 2 ×
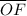
∴ The length of
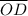 = 2 ×
= 2 ×
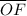 = The length of
= The length of

Given that arc EF = 60°, and the point 'O' is the center of the circle, we have;
∠EOF = The measure of arc EF = 60° = ∠DOB
Therefore, in ΔDOB, we have;
∠D + ∠B = 180° - ∠DOB = 180° - 60° = 120°
∵ ∠D = ∠B, we have;
∠D + ∠B = ∠D + ∠D = 2 × ∠D = 120°
∠D = ∠B = 120°/2 = 60°
All three interior angles of ΔDOB = 60°
∴ ΔDOB is an equilateral triangle and all sides of ΔDOB are equal
Therefore;
The length of
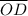 = The length of
= The length of
 = The length of
= The length of
 = 2 ×
= 2 ×
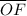
The perimeter of ΔDOB = The length of
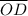 + The length of
+ The length of
 + The length of
+ The length of
 = 2 ×
= 2 ×
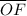 + 2 ×
+ 2 ×
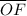 + 2 ×
+ 2 ×
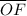 = 6 ×
= 6 ×
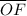
∴ The perimeter of ΔDOB = 6 ×
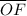
The radius of the circle =
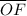 = 6·x
= 6·x
∴ The perimeter of ΔDOB = 6 × 6·x = 36·x