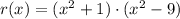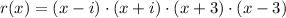Question

Keller performed the work below to express the polynomial in factored form:

r(x) = x4 – 8x2 – 9
r(x) = (x2 + 1)(x2 – 9)
(x) = (x + 1)(x – 1)(x + 3)(x – 3)
Explain the error he made and complete the factorization correctly.

Answer 1

He made the following mistake, he assumed that polynomial
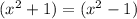`(x^(2)+1) = (x^(2)-1)`, having for granted that
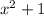`x^(2)+1` has two real roots, instead of two complex roots.

Explanation:

He made the following mistake, he assumed that polynomial
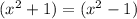`(x^(2)+1) = (x^(2)-1)`, having for granted that
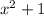`x^(2)+1` has two real roots, instead of two complex roots. The true factorized form of the fourth grade polynomial is:

`r(x) = (x^(2)+1)\cdot (x^(2)-9)`

`r(x) = (x- i)\cdot (x+i)\cdot (x+3)\cdot (x-3)`