Question

A cardboard box manufacturing company is building boxes with length represented by x+1, width by 5 - x, and height by x - 1. The volume of the box is modeled by the function below. a) What is a reasonable domain for V(x)? b) What value of x would produce the greatest volume box? c) For which values of x is the volume increasing?

HELP ASAP!

Answer 1

Part A)

In interval notation:

(1, 5)

Or, as an inequality:

1<x<5

Part B)

x ≈ 3.5

Part C)

V(x) is increasing for 1<x<3.5 and decreasing for 3.5<x<5

`\color{yellow}{}`

Answer 2

Part A)

In interval notation:

`(1, 5)`

Or, as an inequality:

`1<x<5`

Part B)

`x\approx 3.5`

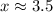
Part C)

V(x) is increasing for 1 < x < 3.5 and decreasing for 3.5 < x < 5.

Explanation:

The building boxes have lengths represented by (x + 1), widths by (5 - x), and heights by (x - 1).

Part A)

Since they are side lengths, they must be positive. In other words:

`\displaystyle x+1>0, 5-x>0\text{ and } x-1>0`

Solving for each inequality yields:

`x>-1, x<5,\text{ and } x>1`

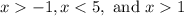
We can eliminate the first inequality. Thus, our compound inequality is:

`1<x<5`

So, the reasonable domain for V(x) will be all values greater than one and less than five.

In interval notation:

`(1, 5)`

Or as an inequality:

`1<x<5`

Part B)

We only need to look at the part of the graph within our domain.

For 1 < x < 5, we can see that its maximum is 17.

This occurs around x = 3.5.

Part C)

Again, we only need to look at the part of the graph within our domain.

As we can see, starting from x = 1 to x = 3.5 (approximately), our function is increasing (i.e. sloping upwards).

From x = 3.5 (approximately) and ending at x = 5, our function is decreasing.

Therefore, V(x) is increasing for 1 < x < 3.5 and decreasing for 3.5 < x < 5.