Answer:
Question 1)
Cristina is traveling 11 miles per hour and Kori is traveling 20 miles per hour.
Question 2)
Four hours.
Question 3)
Paige spent two hours biking and six hours walking.
Explanation:
Question 1)
Let Cristina's speed be x.
Kori travels 9 miles per hour faster than Cristina. So, Kori's speed is (x + 9).
After six hours, Cristina would have traveled 6x miles and Kori would have traveled 6(x + 9) miles.
Since Kori traveled in the opposite direction, we can place a negative to represent this. So, after six hours, Kori is -6(x + 9) miles away from the restaurant while Cristina is 6x miles away from the restaurant.
Since the distance between them is 186 miles, the difference of the two expressions is 186. Hence:
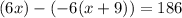
Distribute:
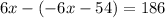
Distribute:
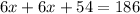
Simplify:

Hence:
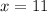
Cristina's speed is 11 miles per hour. Thus, Kori's speed is 20 miles per hour.
Question 2)
Let h represent the amount of time that has passed in hours.
Carrie left the restaurant traveling 12 miles per hour.
Four hours later, Leah left traveling in the same direction at 24 miles per hour.
After four hours, Carrie would have traveled 12(4) = 48 miles.
Carrie would still be traveling at 12 miles per hour. So, her distance from the restaurant is given by:
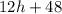
Since Leah just left and is traveling at a rate of 24 miles per hour, her distance from the restaurant is given by:
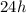
Leah will catch up when the two expressions are equivalent. Hence:
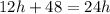
Solve for h:
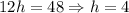
Leah will catch up with Carrie in four hours.
Question 3)
Let x represent the amount of hours spent biking and y represent the amount of hours spent walking.
The total trip to the mall took eight hours. Hence:
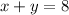
The mall is a total of 46 miles away. Since Paige bikes at a rate of 8 miles per hour and walks at a rate of five miles per hour:
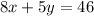
Solve the system. We can use elimination. Multiply the first equation by -5:
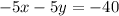
We can add this to the second equation:

Hence:
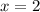
Using the first equation again:
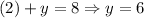
So, Paige spent two hours biking and six hours walking.