The question is incomplete. The complete question is :
The population of a certain town was 10,000 in 1990. The rate of change of a population, measured in hundreds of people per year, is modeled by P prime of t equals two-hundred times e to the 0.02t power, where t is measured in years since 1990. Discuss the meaning of the integral from zero to twenty of P prime of t, d t. Calculate the change in population between 1995 and 2000. Do we have enough information to calculate the population in 2020? If so, what is the population in 2020?
Solution :
According to the question,
The rate of change of population is given as :
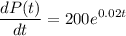 in 1990.
in 1990.
Now integrating,
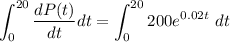
![$=(200)/(0.02)\left[e^(0.02(20))-1\right]$](https://img.qammunity.org/2022/formulas/mathematics/college/eljd9a92knner3amp3n6s7lehh4gofm62m.png)
![$=10,000[e^(0.4)-1]$](https://img.qammunity.org/2022/formulas/mathematics/college/ne7e6409j1hb96ad0rkyjyzp6nd0dxjffi.png)
![$=10,000[0.49]$](https://img.qammunity.org/2022/formulas/mathematics/college/7w8uyemo3ctgxfws07vsh7l9rt0fq7mlvb.png)
=4900
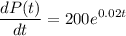
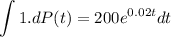
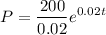
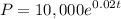

This is initial population.
k is change in population.
So in 1995,

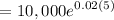
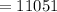
In 2000,

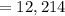
Therefore, the change in the population between 1995 and 2000 = 1,163.