Question

\int\limits^0_∞ cos{x} \, dx

Answer 1

`\displaystyle \int\limits^0_\infty {cos(x)} \, dx = sin(\infty)`

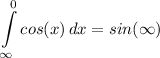
General Formulas and Concepts:

Pre-Calculus

• Unit Circle
• Trig Graphs

Calculus

• Limits
• Limit Rule [Variable Direct Substitution]:
  `\displaystyle \lim_(x \to c) x = c`
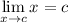
• Integrals
• Integration Rule [Fundamental Theorem of Calculus 1]:
  `\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)`
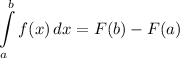
• Trig Integration
• Improper Integrals

Explanation:

Step 1: Define

Identify

`\displaystyle \int\limits^0_\infty {cos(x)} \, dx`

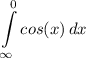
Step 2: Integrate

1. [Improper Integral] Rewrite:
   `\displaystyle \lim_(a \to \infty) \int\limits^0_a {cos(x)} \, dx`
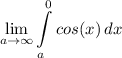
2. [Integral] Trig Integration:
   `\displaystyle \lim_(a \to \infty) sin(x) \bigg| \limits^0_a`
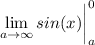
3. [Integral] Evaluate [Integration Rule - FTC 1]:
   `\displaystyle \lim_(a \to \infty) sin(0) - sin(a)`
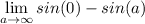
4. Evaluate trig:
   `\displaystyle \lim_(a \to \infty) -sin(a)`
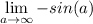
5. Evaluate limit [Limit Rule - Variable Direct Substitution]:
   `\displaystyle -sin(\infty)`

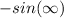
Since we are dealing with infinity of functions, we can do a numerous amount of things:

• Since -sin(x) is a shift from the parent graph sin(x), we can say that -sin(∞) = sin(∞) since sin(x) is an oscillating graph. The values of -sin(x) already have values in sin(x).
• Since sin(x) is an oscillating graph, we can also say that the integral actually equates to undefined, since it will never reach 1 certain value.

∴
`\displaystyle \int\limits^0_\infty {cos(x)} \, dx = sin(\infty) \ or \ \text{unde}\text{fined}`

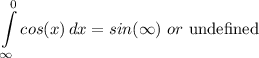
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Improper Integrals

Book: College Calculus 10e