Answer:
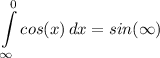
General Formulas and Concepts:
Pre-Calculus
Calculus
- Limits
- Limit Rule [Variable Direct Substitution]:
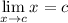
- Integrals
- Integration Rule [Fundamental Theorem of Calculus 1]:
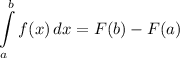
- Trig Integration
- Improper Integrals
Explanation:
Step 1: Define
Identify
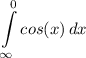
Step 2: Integrate
- [Improper Integral] Rewrite:
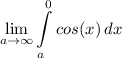
- [Integral] Trig Integration:
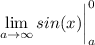
- [Integral] Evaluate [Integration Rule - FTC 1]:
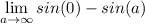
- Evaluate trig:

- Evaluate limit [Limit Rule - Variable Direct Substitution]:
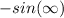
Since we are dealing with infinity of functions, we can do a numerous amount of things:
- Since -sin(x) is a shift from the parent graph sin(x), we can say that -sin(∞) = sin(∞) since sin(x) is an oscillating graph. The values of -sin(x) already have values in sin(x).
- Since sin(x) is an oscillating graph, we can also say that the integral actually equates to undefined, since it will never reach 1 certain value.
∴
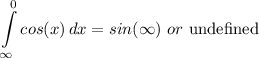
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Improper Integrals
Book: College Calculus 10e