Question

You are to play the following game of cards. Cards are worth their face value, Jacks, Queens and Kings are also worth 10 and Aces are worth 11. You pull precisely two cards from a standard deck and if their sum is at least 20, then you win the game and are given a prize of cash. It costs you $10 to play the game. At least how much should the prize be in order to make your expected winnings positive

Answer 1

$82.875

Explanation:

From the given information:

Assume F is used to denote the two cards;

If there are four aces among 52 playing cards, the chance of selecting the first ace is =
`(4)/(52)`

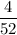
After selecting the first ace, we have only 3 aces remaining and a total of 51 playing cards. Thus, the chance of selecting the second ace will be
`(3)/(51)`

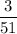
By applying product rule, we can determine the chance of selecting two aces without replacement as follows:

i.e.

`P(F=22)=(4)/(52)* (3)/(51)`

`= (1)/(221)`

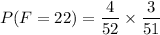
The probability of getting one ace, one face is:

`P(F=21) =( (4)/(52)* (12)/(51))+( (12)/(52)* (4)/(51))`

`P(F=21) = (4)/(221)*(4)/(221)`

`P(F=21) = (8)/(221)`

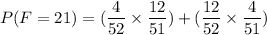
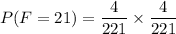
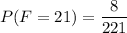
Since there are 4 aces, 4 nine, and 12 faces in a card deck

The probability of getting one ace, one nine, or two faces now will be:

`P(F=20) = ((4)/(52) * (4)/(51))+ ((4)/(52) * (4)/(51)) + ((12)/(52) * (11)/(51))`

`P(F=20) = ((53)/(663) )`

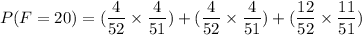
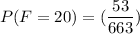
Now, the probability of at least 20 now is:

`\text{P(F at least 20)} = (1)/(221)+(8)/(221)+(53)/(663)`

`\text{P(F at least 20)} = (80)/(663)`

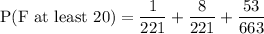
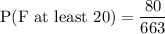
If H represents the amount of prize of the expected winnings:

Then;

`(H - 10) ((80)/(663)) + (-10)((663-80)/(663)) = 0`

`(80(H-10))/(663)-(5830)/(663)=0`

`(80(H-10))/(663)=(5830)/(663)`

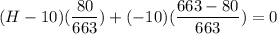
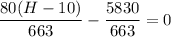
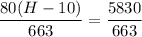
80H - 800 = 5830

80H = 5830 +800

80H = 6630

H = 6630/80

H = $82.875

The prize should be $82.875 to make a winning positive.