Question

The interarrival time of nuclear particles in a Monte Carlo simulation of a reaction is designed to have a uniform distribution over an interval from 0 to 0.5 milliseconds. Determine the probability that the interarrival time between two particles will be:

Answer 1

Incomplete question, but you can use the formulas given to solve it.

Explanation:

Uniform probability distribution:

An uniform distribution has two bounds, a and b.

The probability of finding a value of at lower than x is:

`P(X < x) = (x - a)/(b - a)`

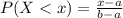
The probability of finding a value between c and d is:

`P(c \leq X \leq d) = (d - c)/(b - a)`

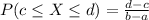
The probability of finding a value above x is:

`P(X > x) = (b - x)/(b - a)`

Uniform distribution over an interval from 0 to 0.5 milliseconds

This means that
`a = 0, b = 0.5`

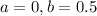
Determine the probability that the interarrival time between two particles will be:

Considering
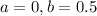`a = 0, b = 0.5`, and the question asked, you choose one of the three formulas above.