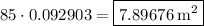Answer:
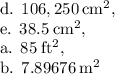
Explanation:
Part D:
The figure shows a parallelogram with base 425 cm and height 250 cm. Its area can be found by
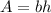 and therefore the area of this shape is
and therefore the area of this shape is
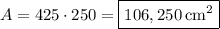
Part E:
The figure shows a trapezoid. The area of a trapezoid is equal to the average of its bases multiplied by the height. Since one base is 2 cm and the other base is 9 cm, the average of these bases is
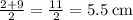 . The height is given as 7 cm, therefore the area of the trapezoid is
. The height is given as 7 cm, therefore the area of the trapezoid is

Part A:
The composite figure consists of two rectangles. The area of a rectangle with base
 and height
and height
 is given by
is given by
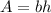 . The total area of the figure is equal to the sum of the areas of these two rectangles.
. The total area of the figure is equal to the sum of the areas of these two rectangles.
Area of first rectangle (rectangle on bottom):
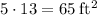
Area of second rectangle (rectangle on top):
*Since we don't know the dimensions, we must find them. Start by converting 108 inches to feet:
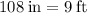 . Therefore, the dimensions of this rectangle are (10-5) ft by (13-9) ft
. Therefore, the dimensions of this rectangle are (10-5) ft by (13-9) ft
 and this rectangle's area is
and this rectangle's area is
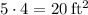
Thus, the area of the figure is equal to
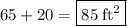
Part B:
We've already found the area of the figure in the previous part in square feet. To find the area in square meters, use the conversion
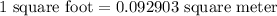 .
.
Therefore, the area of the figure, in square meters, is