✏️ Development:
✍ Having as t₃ =10 and t₁₀ = -4. We have to find the common ratio.
❑ If, in front of the sequence from 3 to 10, there are 7 numbers, that is, 7 terms, we have to find a pattern, what I used was this one.

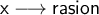
We see that in the calculation, the only number that fits is -2.
➤ Because if we stop to think about it, we have -2 of common ratio among these 7 terms is -14, so 10-14 = -4
So the hypothesis is correct!
➜ Being right as -2 and resuming the terms of 10, we have:

So t₁₂ is equal to -8.
⊱───────────⊰✯⊱────────⊰