Question

Consider the given function. Plot the x-intercept(s), y-intercept, vertex, and axis of symmetry of the function.

Answer 1

Following are the solution to the gvien question:

Explanation:

Let the quadratic equation is:

`\to h(x) = (x + 1)^2 - 4`

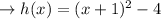
vertex is:

`\to h(x) = a(x -h)^2 + k`

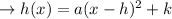
(h) = axis of symmetry

(h,k) = vertex.

By using the given equation:

`h(x) = (x - (-1))^2 - 4`

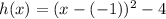
Hence,

`h = -1 \\\\ k = -4`

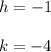
line of symmetry
`x = -1`

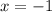
vertex is
`(h,k) = (-1,-4)`

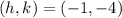
finding the x intercept:

`(x + 1)^2 = 4\\\\√((x + 1)^2) = √(4)\\\\x + 1 = \pm 2\\\\x = 2-1 \ \ \ \ \ \ \ \ \ \ or \ \ \ \ \ \ \ \ \ \ \ \ \ \ x =-2 -1\\\\x = 1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ or \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x =-3\\\\`

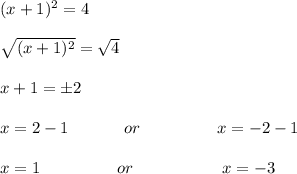
x -intercepts -3,1

Calculating the y-intercept when x = 0 putting into the real equation:

`h(x) = (0 +1)^2 - 4 \\\\y = 1 - 4\\\\y = -3`

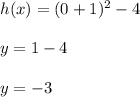
Please find the graph file in the attachment.