Answer:
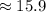
Explanation:
The length of an arc with measure
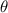 and radius
and radius
 is given by
is given by
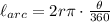 . From the figure, we know that the radius of arc ADC is 4, but we don't know the measure of the arc. Since there are 360 degrees in a circle, the measure of arc ADC is equal to the measure of the arc formed by
. From the figure, we know that the radius of arc ADC is 4, but we don't know the measure of the arc. Since there are 360 degrees in a circle, the measure of arc ADC is equal to the measure of the arc formed by
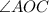 subtracted from 360. The measure of the arc formed by
subtracted from 360. The measure of the arc formed by
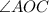 consists of two congruent angles,
consists of two congruent angles,
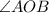 and
and
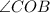 . To find them, we can use basic trigonometry for a right triangle, since by definition, tangents intersect a circle at a right angle.
. To find them, we can use basic trigonometry for a right triangle, since by definition, tangents intersect a circle at a right angle.
In any right triangle, the cosine of an angle is equal to its adjacent side divided by the hypotenuse, or longest side, of the triangle.
We have:
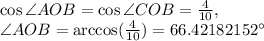
Therefore,
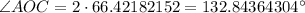
The measure of the central angle of
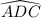 must then be
must then be
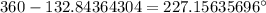
Thus, the length of
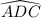 is equal to:
is equal to:
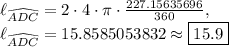 (three significant figures as requested by question).
(three significant figures as requested by question).