Question

I really need this question someone please help ​

Answer 1

`\approx 15.9`

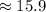
Explanation:

The length of an arc with measure
`\theta` and radius
`r` is given by
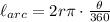`\ell_(arc)=2r\pi\cdot (\theta)/(360)`. From the figure, we know that the radius of arc ADC is 4, but we don't know the measure of the arc. Since there are 360 degrees in a circle, the measure of arc ADC is equal to the measure of the arc formed by
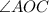`\angle AOC` subtracted from 360. The measure of the arc formed by
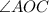`\angle AOC` consists of two congruent angles,
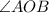`\angle AOB` and
`\angle COB`. To find them, we can use basic trigonometry for a right triangle, since by definition, tangents intersect a circle at a right angle.

In any right triangle, the cosine of an angle is equal to its adjacent side divided by the hypotenuse, or longest side, of the triangle.

We have:

`\cos \angle AOB=\cos \angle COB=(4)/(10),\\\angle AOB=\arccos((4)/(10))=66.42182152^(\circ)`

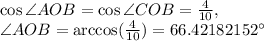
Therefore,
`\angle AOC=2\cdot 66.42182152=132.84364304^(\circ)`

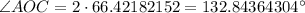
The measure of the central angle of
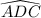`\widehat{ADC}` must then be
`360-132.84364304=227.15635696^(\circ)`

Thus, the length of
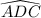`\widehat{ADC}` is equal to:

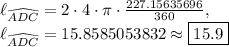`\ell_{\widehat{ADC}}=2\cdot 4\cdot \pi \cdot (227.15635696)/(360),\\\ell_{\widehat{ADC}}=15.8585053832\approx \boxed{15.9}` (three significant figures as requested by question).