Question

An airplane flies between two points on the ground that are 500 km apart. The destination is directly north of the point of origin of the flight. The plane flies with an airspeed of 120 m/s. If a constant wind blows at 10 m/s toward the west during the flight, what direction must the plane fly relative to the air to arrive at the destination

Answer 1

The right solution is "4.8° east of north".

Step-by-step explanation:

Given:

Distance,

= 500 km

Speed,

`\vec{v}=120 \ m/s`

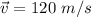
Wind (towards west),

`v_0=10 \ m/s`

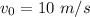
According to the question, we get

The angle will be:

⇒
`\Theta=Cos^(-1)((v_0)/(v_1) )`

`=Cos^(-1)((10)/(120) )`

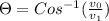
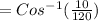
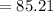`=85.21` (north of east)

hence,

The direction must be:

⇒
`\Theta'=90-85.21`

`=4.79^(\circ)`

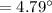
or,

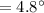`=4.8^(\circ)` (east of north)