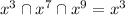Answer:
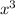
Explanation:
Let the greatest common factor of
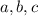 such that
such that
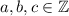 and they are not all equal to zero,
and they are not all equal to zero,
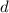 is the common divisor of
is the common divisor of
 and
and
 . Therefore,
. Therefore,
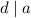 and
and
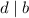
You can write
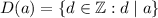

The greatest common factor of
 is given as
is given as
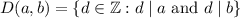
and
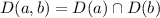
This happens because
 is upper bounded because if
is upper bounded because if
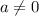 then
then
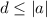
for all
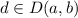 . Therefore, the set
. Therefore, the set
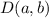 has the greatest elements.
has the greatest elements.
Taking
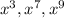 such that
such that

You can note that
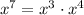 and
and
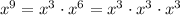
Therefore, the greatest common factor is
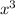
Note: