Question

PLEASE HELP!! i’m so confused.

Answer 1

[A] -0.5

General Formulas and Concepts:

Algebra I

• Reading a coordinate plane
• Coordinates (x, y)
• Functions
• Function Notation

Algebra II

• Piecewise Functions

Calculus

Limits

Graphical Limits

Discontinuities

• Removable (Hole)
• Jump
• Infinite (Asymptote)

Explanation:

Step 1: Define

Identify

`\displaystyle f(x) = \left \{ {{-1 - x, \ x \\eq 2} \atop {8, \ x = 2}} \right.`

`\displaystyle \lim_(x \to -0.5) f(x)`

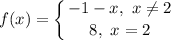
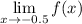
Step 2: Solve

According to the graph, we see that when we approach x = -0.5 of the function f(x), we land on y = -0.5.

The function value at x = 2 would equal 8, but the limit as x approaches -0.5 would not approach the function value, but approach the hole in the function.

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Limits

Book: College Calculus 10e