Question

I need help finding the distince.​

Answer 1

guessing that the area of the inner rectangle is 10m²

and the other rectangle is 16m*10m= 160m²

we can say that

(16-x) * (10-x) = 10

for the area of the inner rectangle

let's calculate the lefthand side of the equation

160 - 16x -10x + x² = 10

160 -26x +x² = 10

subtract 10 on both sides

150 -26x +x² = 0

rearrange

x² -26x + 150 = 0

looks like something we can throw the pq formula on to solve for x

with p = -26 and q = 150

`x = - ( - 26)/(2) ( + )/( - ) \sqrt{( ( - 26)/(2))^(2) - 150 }`

`x = 13 ( + )/( - ) √(169 - 150 )`

`x = 13 ( + )/( - ) √(19 )`

`x1 = 8.64`

`x2 =17.36`

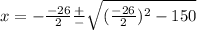
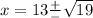
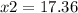
we need to interpret this solutions

but to be sure on this, I need the unreadable text of the photographed problem