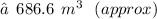
The above figure consists of three different shapes, that is :
- A hemisphere
- A Cylinder
- A Cone
Let's solve for surface area of whole figure :
1. Curved surface area of hemisphere : -
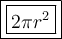
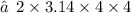
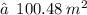
2. lateral surface area of Cylinder : -
- radius (r) = 4 m
- height (h) = 10 m
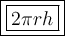
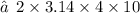
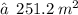
3. curved surface area of cone :
- radius (r) = 4 m
- height of cone (h') = 3 m.
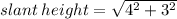
(by Pythagoras theorem)
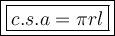
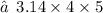
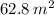
Surface area of the figure :
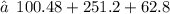
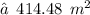
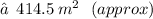
Now, let's solve for volume :
Volume of given figure will be combined volume of the all three shapes,
1. Volume of hemisphere :
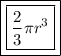
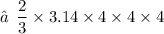
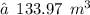
2. Volume of Cylinder :
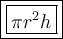
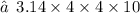
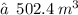
3. Volume of cone :
- height of cone (h') = 3 m
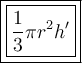
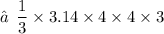
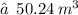
The total volume of the given figure :
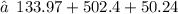
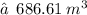
or