Question

Suppose that 10% of the undergraduates at a certain university are foreign students, and that 25% of the graduate students are foreign. If there are four times as many undergraduates as graduate students, given that a randomly selected student is foreign, what is the probability that the student is an undergraduate

Answer 1

0.6154 = 61.54% probability that the student is an undergraduate

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: Foreign

Event B: Undergraduate.

There are four times as many undergraduates as graduate students

So 4/5 = 80% are undergraduate students and 1/5 = 20% are graduate students.

Probability the student is foreign:

10% of 80%

25% of 20%. So

`P(A) = 0.1*0.8 + 0.25*0.2 = 0.13`

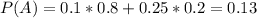
Probability that a student is foreign and undergraduate:

10% of 80%. So

`P(A \cap B) = 0.1*0.8 = 0.08`

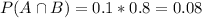
What is the probability that the student is an undergraduate?

`P(B|A) = (P(A \cap B))/(P(A)) = (0.08)/(0.13) = 0.6154`

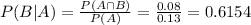
0.6154 = 61.54% probability that the student is an undergraduate