Answer:
[C] 0
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Distributive Property
Algebra I
- Terms/Coefficients
- Functions
- Function Notation
Calculus
Limits
Derivatives
Definition of a Derivative:

Explanation:
Step 1: Define
Identify

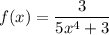
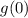
Step 2: Differentiate
- Substitute in x [Function g(x)]:

- Substitute in function f(x) [Function g(x)]:

- Simplify:

- Rewrite:
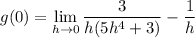
- Rewrite:
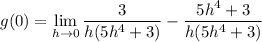
- [Subtraction] Combine like terms:
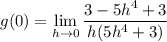
- [Addition] Simplify:
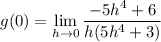
- [Distributive Property] Distribute h:
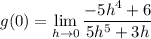
- Evaluate limit [Power Method]:
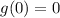
Since the bottom polynomial has a higher degree than the top polynomial, the bottom polynomial will increase faster.
∴ If the bottom is approaching a bigger value, the fraction gets smaller and smaller, approaching 0.
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Derivatives
Book: College Calculus 10e